Вопросы:
- В каком состоянии сейчас находится проблема
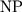 -полноты? Возможно ли где-нибудь ознакомиться
с результатами последних исследований в данной области
(предпочтительны русскоязычные материалы). Уже достаточно давно
встречаю в Сети подобные ресурсы: http://www.tarusa.ru/~mit/RUS/rus.php,
но, к сожалению, не вижу результата подобных заявлений.
-полноты? Возможно ли где-нибудь ознакомиться
с результатами последних исследований в данной области
(предпочтительны русскоязычные материалы). Уже достаточно давно
встречаю в Сети подобные ресурсы: http://www.tarusa.ru/~mit/RUS/rus.php,
но, к сожалению, не вижу результата подобных заявлений.
- Интересует задача факторизации больших чисел и ее соотношение с
классом
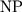 -полных задач. На вышеупомянутом
ресурсе по ссылке http://www.tarusa.ru/~mit/RUS/crypt.php
можно найти информацию о том, что задача факторизации и
-полных задач. На вышеупомянутом
ресурсе по ссылке http://www.tarusa.ru/~mit/RUS/crypt.php
можно найти информацию о том, что задача факторизации и
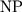 -полные задачи (приведен пример задачи
ВЫПОЛНИМОСТЬ) имеют одинаковый порядок роста сложности по входным
данным. На основании этого косвенно можно предположить, что задача
факторизации является
-полные задачи (приведен пример задачи
ВЫПОЛНИМОСТЬ) имеют одинаковый порядок роста сложности по входным
данным. На основании этого косвенно можно предположить, что задача
факторизации является 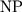 -полной. Кто-нибудь
занимается или занимался вопросами доказательства отнесения задачи
факторизации к классу
-полной. Кто-нибудь
занимается или занимался вопросами доказательства отнесения задачи
факторизации к классу 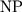 -полных задач? Хотелось
бы услышать на этот счет авторитетное мнение.
-полных задач? Хотелось
бы услышать на этот счет авторитетное мнение.
- Чисто гипотетический вопрос. Что изменится в теоретической и
прикладной криптографии в случае доказательства соотношения
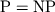 (т. е. отыскания
полиномиального алгоритма для какой-либо
(т. е. отыскания
полиномиального алгоритма для какой-либо
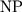 -полной задачи)?
-полной задачи)?
Ответы:
1. По-видимому вопрос сформулирован не совсем точно и речь
идет не о проблеме ![]() -полноты, а о знаменитой
проблеме соотношения классов
-полноты, а о знаменитой
проблеме соотношения классов ![]() и
и ![]() .
.
Впрочем, в теории сложности вычислений есть область исследований,
которую можно было бы назвать проблемой
![]() -полноты. Здесь следует отметить, что
общеизвестный и широко используемый термин
"
-полноты. Здесь следует отметить, что
общеизвестный и широко используемый термин
"![]() -полная задача" с математической точки зрения
не вполне корректен. Полнота определяется для пары (класс сложностей,
тип сводимости) и математически строгое определение говорит о задаче,
полной в данном классе относительно данного типа сводимости. Уже в
своих основополагающих работах Кук и Карп использовали разные типы
сводимости. Существуют и другие сводимости, в т. ч., например,
рандомизированные. Каждый тип сводимости определяет свое множество
задач, полных в классе
-полная задача" с математической точки зрения
не вполне корректен. Полнота определяется для пары (класс сложностей,
тип сводимости) и математически строгое определение говорит о задаче,
полной в данном классе относительно данного типа сводимости. Уже в
своих основополагающих работах Кук и Карп использовали разные типы
сводимости. Существуют и другие сводимости, в т. ч., например,
рандомизированные. Каждый тип сводимости определяет свое множество
задач, полных в классе ![]() . Вопрос о
соотношениях между такими множествами (совпадают или различаются) во
многих случаях остается открытым и с полным основанием может
называться проблемой
. Вопрос о
соотношениях между такими множествами (совпадают или различаются) во
многих случаях остается открытым и с полным основанием может
называться проблемой ![]() -полноты. Подчеркнем, что
эта проблема представляет интерес главным образом в контексте
исследования структуры класса
-полноты. Подчеркнем, что
эта проблема представляет интерес главным образом в контексте
исследования структуры класса ![]() . Когда же
речь идет о сложности какой-либо конкретной задачи
. Когда же
речь идет о сложности какой-либо конкретной задачи ![]() , то
достаточно продемонстрировать произвольную (полиномиальную,
детерминированную) сводимость, скажем, задачи ВЫПОЛНИМОСТЬ к
, то
достаточно продемонстрировать произвольную (полиномиальную,
детерминированную) сводимость, скажем, задачи ВЫПОЛНИМОСТЬ к
![]() . Это будет свидетельством вычислительной сложности
задачи
. Это будет свидетельством вычислительной сложности
задачи ![]() в том смысле, что из существования для нее
полиномиального детерминированного алгоритма будет следовать, что
в том смысле, что из существования для нее
полиномиального детерминированного алгоритма будет следовать, что
![]() .
.
Теперь о проблеме соотношения классов ![]() и
и ![]() . На данный момент она является одной
из наиболее важных и наиболее популярных нерешенных математических
проблем. С сожалением приходится констатировать, что проблема эта
стала даже слишком популярной. Не будет большим преувеличением
сказать, что ферматисты XXI века доказывают, что
. На данный момент она является одной
из наиболее важных и наиболее популярных нерешенных математических
проблем. С сожалением приходится констатировать, что проблема эта
стала даже слишком популярной. Не будет большим преувеличением
сказать, что ферматисты XXI века доказывают, что
![]() . Работы с такими
"доказательствами" публикуются регулярно и, как правило, несут на себе
печать "синдрома непризнанного гения": безудержное самовосхваление,
претензии на какие-то выдающиеся открытия, позволяющие одним махом
решить все мировые проблемы, и, главное, отсутствие корректных
определений и доказательств. Гораздо реже "доказательства" утверждения
. Работы с такими
"доказательствами" публикуются регулярно и, как правило, несут на себе
печать "синдрома непризнанного гения": безудержное самовосхваление,
претензии на какие-то выдающиеся открытия, позволяющие одним махом
решить все мировые проблемы, и, главное, отсутствие корректных
определений и доказательств. Гораздо реже "доказательства" утверждения
![]() публикуются достаточно
квалифицированными математиками, просто допустившими какой-либо
просмотр в своих рассуждениях. И уж совсем редко встречаются работы, в
которых предпринимаются попытки (также несостоятельные) доказать, что
публикуются достаточно
квалифицированными математиками, просто допустившими какой-либо
просмотр в своих рассуждениях. И уж совсем редко встречаются работы, в
которых предпринимаются попытки (также несостоятельные) доказать, что
![]() .
.
Безусловно, ведутся в связи с этой проблемой и серьезные
исследования, но, как уже было сказано выше, проблема соотношения
классов ![]() и
и ![]() остается
открытой. Тем не менее, на наш взгляд, состояние исследований этой
проблемы и "вокруг нее" заслуживает несколько более подробного
обсуждения на нашем сайте.
остается
открытой. Тем не менее, на наш взгляд, состояние исследований этой
проблемы и "вокруг нее" заслуживает несколько более подробного
обсуждения на нашем сайте.
Прежде всего о литературе. Всем известна монография Гэри и Джонсона [1]. Некоторую дополнительную информацию можно найти в книге [2]. На русском языке никаких изданий с более полным освещением данной проблематики нам не известно. Более того, и англоязычные первоисточники в нашей стране труднодоступны. Основные результаты докладываются на специализированной конференции STRUCTURE (IEEE Structure in Complexity Theory Conference), а также на двух самых престижных международных симпозиумах по математической кибернетике: STOC (ACM Symposium on Theory of Computing) и FOCS (IEEE Symposium on the Foundations of Computer Science). Проблема труднодоступности первоисточников весьма серьезна, так, например, для некоторых из цитируемых ниже работ мы не можем даже указать номера страниц! (Ситуация с литературой по математической криптографии не намного лучше, поскольку наиболее значительные результаты публикуются в основном в трудах все тех же симпозиумов STOC и FOCS).
Все используемые ниже и необъясняемые в тексте понятия можно найти в книгах [1], [2].
Начнем с замечания, что в теории сложности существуют и другие не
менее интересные и трудные проблемы. Вопрос о соотношении классов
![]() и
и ![]() --- это часть
общей проблемы соотношения между детерминированными и
недетерминированными вычислениями. А имеется еще, например, и
любопытная проблема соотношения ограничений на время и ограничений на
память. Через
--- это часть
общей проблемы соотношения между детерминированными и
недетерминированными вычислениями. А имеется еще, например, и
любопытная проблема соотношения ограничений на время и ограничений на
память. Через ![]() (
(![]() ) обозначается класс языков,
распознаваемых детерминированными машинами Тьюринга на полиномиальной
(логарифмической) памяти. Следующая цепочка включений почти очевидна.
) обозначается класс языков,
распознаваемых детерминированными машинами Тьюринга на полиномиальной
(логарифмической) памяти. Следующая цепочка включений почти очевидна.
![]() .
.
Но вопрос о том, какие из трех включений в данной цепочке являются
строгими, остается открытым. Известно, что класс
![]() шире класса
шире класса
![]() (так называемая теорема об иерархии).
Поэтому хотя бы одно из этих трех включений должно быть строгим.
Можно предположить, что все три являются таковыми. Тогда, вроде бы,
следует сначала взяться за более "легкую" задачу --- отделить
класс
(так называемая теорема об иерархии).
Поэтому хотя бы одно из этих трех включений должно быть строгим.
Можно предположить, что все три являются таковыми. Тогда, вроде бы,
следует сначала взяться за более "легкую" задачу --- отделить
класс ![]() от
от ![]() .
Соотношение этих классов --- еще одна из центральных нерешенных
проблем теории сложности.
.
Соотношение этих классов --- еще одна из центральных нерешенных
проблем теории сложности.
Также заслуживает пристального внимания и проблема соотношения
вероятностных и недетерминированных вычислений и соответствующих
классов сложностей. Очевидно, что
![]() (
(![]() --- вероятностный аналог класса
--- вероятностный аналог класса
![]() ). Неспециалисты в теории сложности почему-то
убеждены, что
). Неспециалисты в теории сложности почему-то
убеждены, что ![]() . На самом
деле, ни это включение, ни противоположное ему
(
. На самом
деле, ни это включение, ни противоположное ему
(![]() ), на данный момент не
доказаны. Статус класса
), на данный момент не
доказаны. Статус класса ![]() вообще весьма
любопытен. Известно, что
вообще весьма
любопытен. Известно, что ![]() (см. [3]). Здесь
(см. [3]). Здесь
![]() --- класс второго уровня полиномиальной
иерархии. При этом не доказано даже, что класс
--- класс второго уровня полиномиальной
иерархии. При этом не доказано даже, что класс
![]() шире чем
шире чем ![]() (класс
(класс
![]() определяется аналогично классу
определяется аналогично классу
![]() с заменой ограничений вида
с заменой ограничений вида
![]() на ограничения вида
на ограничения вида ![]() ). С
другой стороны, ведутся исследования по дерандомизации эффективных
вероятностных алгоритмов. Сформулирована гипотеза (некоторым
специалистам она кажется правдоподобной), при которой
). С
другой стороны, ведутся исследования по дерандомизации эффективных
вероятностных алгоритмов. Сформулирована гипотеза (некоторым
специалистам она кажется правдоподобной), при которой
![]() [4].
[4].
За прошедшие годы были опубликованы многочисленные работы,
посвященные исследованиям релятивизированных классов сложностей,
подтвердившим, косвенным образом, трудность указанных
проблем. Например, построены оракулы ![]() и
и ![]() такие, что
такие, что ![]() , но
, но
![]() [5]. Этот результат показывает, что проблема
соотношения классов
[5]. Этот результат показывает, что проблема
соотношения классов ![]() и
и ![]() не может быть решена никаким методом, допускающим релятивизацию (а
таких в математике подавляющее большинство). По-видимому, совсем уж
неожиданным, на первый взгляд, должен показаться следующий результат:
существует оракул
не может быть решена никаким методом, допускающим релятивизацию (а
таких в математике подавляющее большинство). По-видимому, совсем уж
неожиданным, на первый взгляд, должен показаться следующий результат:
существует оракул ![]() такой, что
такой, что
![]() [6].
[6].
Существует следующий вполне очевидный путь для отделения класса
![]() от
от ![]() : взять какую-либо
: взять какую-либо
![]() -полную задачу и доказать для нее
сверхполиномиальную нижнюю оценку сложности. Ввиду известной
двойственности между машинами Тьюринга и схемами из функциональных
элементов, можно использовать любую из этих моделей вычислений. По
ряду причин, которые мы здесь обсуждать не будем, схемы представляются
более удобной моделью для исследования проблемы нижних границ
сложности. Так вот, насколько нам известно, на данный момент наиболее
высокая нижняя оценка схемной сложности для конкретной
(индивидуальной) функции имеет порядок
-полную задачу и доказать для нее
сверхполиномиальную нижнюю оценку сложности. Ввиду известной
двойственности между машинами Тьюринга и схемами из функциональных
элементов, можно использовать любую из этих моделей вычислений. По
ряду причин, которые мы здесь обсуждать не будем, схемы представляются
более удобной моделью для исследования проблемы нижних границ
сложности. Так вот, насколько нам известно, на данный момент наиболее
высокая нижняя оценка схемной сложности для конкретной
(индивидуальной) функции имеет порядок ![]() , где
, где
![]() --- длина входа [7].
Подчеркнем, что это --- весьма нетривиальный результат.
--- длина входа [7].
Подчеркнем, что это --- весьма нетривиальный результат.
Так в чем же причина, почему прогресс за три десятилетия в решении
такой интересной и важной проблемы столь незначителен? Разумеется,
пока проблема соотношения классов ![]() и
и
![]() не решена, точного и окончательного ответа на
этот вопрос не будет. Можно высказать лишь гипотезу. Обратимся к
другим разделам математики и посмотрим, чем они занимаются. Что нам
известно, к примеру, о функциях, отображающих отрезок
не решена, точного и окончательного ответа на
этот вопрос не будет. Можно высказать лишь гипотезу. Обратимся к
другим разделам математики и посмотрим, чем они занимаются. Что нам
известно, к примеру, о функциях, отображающих отрезок
![]() в себя? Только то, что почти всякая функция
разрывна почти всюду. Математический анализ изучает только те функции,
которые обладают достаточной гладкостью. Такие функции составляют лишь
ничтожную долю множества всех функций, но обладают хорошими
свойствами, позволяющими применять методы, наработанные на данный
момент. А что знает математика о произвольном множестве, пусть даже
конечном? Тоже практически ничего. В алгебре же изучаются множества,
наделенные хорошей, "удобной" структурой: группы, кольца и т. п.
в себя? Только то, что почти всякая функция
разрывна почти всюду. Математический анализ изучает только те функции,
которые обладают достаточной гладкостью. Такие функции составляют лишь
ничтожную долю множества всех функций, но обладают хорошими
свойствами, позволяющими применять методы, наработанные на данный
момент. А что знает математика о произвольном множестве, пусть даже
конечном? Тоже практически ничего. В алгебре же изучаются множества,
наделенные хорошей, "удобной" структурой: группы, кольца и т. п.
В самой же постановке проблемы отделения класса
![]() от
от ![]() стоит квантор
всеобщности по множеству всех полиномиальных детерминированных
алгоритмов: никакой из этих алгоритмов не распознает
стоит квантор
всеобщности по множеству всех полиномиальных детерминированных
алгоритмов: никакой из этих алгоритмов не распознает
![]() -полный язык. Вероятно в том и состоит
основная трудность указанных выше проблем теории сложности вычислений,
что необходимо исследовать общее свойство элементов из очень большого
и весьма неоднородного множества. И невозможно "спрятаться" ни за
бесконечностью, ни за непрерывностью, ни за "удобной"
структурой. Поэтому проблемы теории сложности, такие как соотношение
классов
-полный язык. Вероятно в том и состоит
основная трудность указанных выше проблем теории сложности вычислений,
что необходимо исследовать общее свойство элементов из очень большого
и весьма неоднородного множества. И невозможно "спрятаться" ни за
бесконечностью, ни за непрерывностью, ни за "удобной"
структурой. Поэтому проблемы теории сложности, такие как соотношение
классов ![]() и
и ![]() , остаются
серьезным, наверное даже основным, вызовом математикам всего мира.
, остаются
серьезным, наверное даже основным, вызовом математикам всего мира.
Вопреки распространенному мнению математиков, неспециалистов в теории сложности вычислений, положение дел с нижними оценками сложности конкретных задач не отличается принципиально от состояния исследований в других областях математики. Стоит ограничить класс рассматриваемых эффективных алгоритмов, как . . . Нет, ничего не становится очевидным или элементарным, но нетривиальные результаты появляются. Так, А. А. Разборов [8] получил сверхполиномиальную нижнюю оценку сложности для конкретной функции в классе монотонных схем, т. е. схем в базисе И, ИЛИ (такие схемы могут вычислять только монотонные функции). Вскоре этот результат был усилен А. Е. Андреевым [9], доказавшим экспоненциальную оценку. Для схем фиксированной глубины сверхполиномиальные нижние оценки были получены Ферстом и др. [10] и Айтаи [11]. Они также в дальнейшем были усилены до экспоненциальных в работах Яо [12] и Хостада [13]. Подчеркнем, что все эти результаты не потребовали изобретения каких-либо искусственных примеров функций. Например, упомянутые нижние оценки сложности схем фиксированной глубины верны для функции четности.
В заключение, о главном вопросе, какого результата в итоге все же
следует ожидать: ![]() или
или
![]() ? Конечно, пока проблема не
решена, никто не даст однозначного ответа. Но все же задумайтесь,
какая из следующих двух ситуаций Вам кажется более правдоподобной:
? Конечно, пока проблема не
решена, никто не даст однозначного ответа. Но все же задумайтесь,
какая из следующих двух ситуаций Вам кажется более правдоподобной:
- эффективные алгоритмы существуют для каждой из тысяч и тысяч
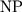 -полных задач, но нам не хватает
изобретательности, чтобы такие алгоритмы придумать.
-полных задач, но нам не хватает
изобретательности, чтобы такие алгоритмы придумать.
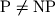 , но на сегодняшний день
математика не располагает методами, позволяющими справиться с
исследованием обширного и неоднородного множества всех полиномиальных
алгоритмов.
, но на сегодняшний день
математика не располагает методами, позволяющими справиться с
исследованием обширного и неоднородного множества всех полиномиальных
алгоритмов.
2. По-видимому, под порядком роста сложности в вопросе понимается оценка сверху.
Еще в 1981 г. Шамир и Шреппель [14]
предложили алгоритм, решающий некоторые
![]() -полные задачи за время
-полные задачи за время
![]() на памяти
на памяти ![]() , где
, где
![]() --- длина входа. Никаких дальнейших продвижений в
данном направлении нам неизвестно.
--- длина входа. Никаких дальнейших продвижений в
данном направлении нам неизвестно.
Что же касается задачи факторизации целых чисел, то уже тривиальный
перебор дает ту же оценку ![]() , что и в
цитированном результате [14]. Здесь
, что и в
цитированном результате [14]. Здесь
![]() --- длина двоичной записи факторизуемого
числа. Имеются и более быстрые алгоритмы, например, с оценкой
--- длина двоичной записи факторизуемого
числа. Имеются и более быстрые алгоритмы, например, с оценкой
![]() . Но в целом, можно сказать, что сложность
детерминированных алгоритмов для задачи факторизации остается мало
исследованной. Это высказывание, казалось бы, противоречит тому факту,
что в многочисленных публикациях по криптографии задаче факторизации
уделяется достаточно внимания и приводятся оценки ее сложности вида
. Но в целом, можно сказать, что сложность
детерминированных алгоритмов для задачи факторизации остается мало
исследованной. Это высказывание, казалось бы, противоречит тому факту,
что в многочисленных публикациях по криптографии задаче факторизации
уделяется достаточно внимания и приводятся оценки ее сложности вида
![]() . Однако, во-первых, все это относится
к вероятностным алгоритмам, а во-вторых, большинство оценок остаются
недоказанными "правдоподобными гипотезами". Более подробно на
алгоритмах факторизации мы не останавливаемся, поскольку
заинтересованный читатель может ознакомиться с данной темой по книге
О. Н. Василенко [15].
. Однако, во-первых, все это относится
к вероятностным алгоритмам, а во-вторых, большинство оценок остаются
недоказанными "правдоподобными гипотезами". Более подробно на
алгоритмах факторизации мы не останавливаемся, поскольку
заинтересованный читатель может ознакомиться с данной темой по книге
О. Н. Василенко [15].
Разумеется, сложность наилучшего из известных алгоритмов для
какой-либо задачи, даже если она очень высока, ничего не говорит о ее
![]() -полноте.
-полноте.
На вопрос о том, является ли задача факторизации
![]() -полной, можно ответить коротко и чисто
формально: безусловно, нет. Напомним, что \mathrm{NP} --- это
класс языков, или, иначе, задач распознавания (decision
problem). Задача факторизации --- это задача поиска решения
(search problem) и она, по определению, не может принадлежать классу
-полной, можно ответить коротко и чисто
формально: безусловно, нет. Напомним, что \mathrm{NP} --- это
класс языков, или, иначе, задач распознавания (decision
problem). Задача факторизации --- это задача поиска решения
(search problem) и она, по определению, не может принадлежать классу
![]() . Но тем не менее, немного изменив подход,
вопрос о
. Но тем не менее, немного изменив подход,
вопрос о ![]() -полноте можно поставить вполне
корректно. Например, вместо задачи поиска сомножителей можно
рассматривать задачу распознавания языка
-полноте можно поставить вполне
корректно. Например, вместо задачи поиска сомножителей можно
рассматривать задачу распознавания языка
![]() , где
, где ![]() ,
если
,
если ![]() --- составное целое число и
--- составное целое число и ![]() -ый
бит его максимального множителя равен
-ый
бит его максимального множителя равен ![]() . Очевидно,
что задача факторизации и задача распознавания языка
. Очевидно,
что задача факторизации и задача распознавания языка ![]() полиномиально эквивалентны. Альтернативно, можно рассматривать
функциональные классы сложностей, состоящие из задач поиска
решения. Например, задача ВЫПОЛНИМОСТЬ ставится так: дана булева
формула, требуется найти набор значений переменных, на котором эта
формула принимает значение
полиномиально эквивалентны. Альтернативно, можно рассматривать
функциональные классы сложностей, состоящие из задач поиска
решения. Например, задача ВЫПОЛНИМОСТЬ ставится так: дана булева
формула, требуется найти набор значений переменных, на котором эта
формула принимает значение ![]() . Функциональные аналоги
классов сложностей, как правило, обозначают, добавляя букву F к
соответствующему названию:
. Функциональные аналоги
классов сложностей, как правило, обозначают, добавляя букву F к
соответствующему названию: ![]() ,
,
![]() и т. п. Следует заметить, что
соотношение между сложностью задач поиска решения и соответствующих
задач распознавания представляет собой нетривиальную проблему. Ее
исследование имеет большое значение для теории алгоритмов, теории
сложности и математической криптографии. Но это --- тема для
отдельного разговора.
и т. п. Следует заметить, что
соотношение между сложностью задач поиска решения и соответствующих
задач распознавания представляет собой нетривиальную проблему. Ее
исследование имеет большое значение для теории алгоритмов, теории
сложности и математической криптографии. Но это --- тема для
отдельного разговора.
К моменту возникновения теории ![]() -полноты в
математике было известно довольно много задач, которые решались
тривиальным перебором за экспоненциальное время, и для которых не
удалось найти полиномиальные алгоритмы. Для большинства этих задач
относительно быстро и несложно была установлена
-полноты в
математике было известно довольно много задач, которые решались
тривиальным перебором за экспоненциальное время, и для которых не
удалось найти полиномиальные алгоритмы. Для большинства этих задач
относительно быстро и несложно была установлена
![]() -полнота (или
-полнота (или
![]() -трудность). В некоторых случаях
доказательство
-трудность). В некоторых случаях
доказательство ![]() -полноты потребовало
определенных усилий. Были и такие примеры, когда попытки
доказательства
-полноты потребовало
определенных усилий. Были и такие примеры, когда попытки
доказательства ![]() -полноты не увенчались успехом,
и в конце концов было доказано, что задача принадлежит классу
-полноты не увенчались успехом,
и в конце концов было доказано, что задача принадлежит классу
![]() (как в случае задачи линейного
программирования). А несколько задач, как говорится, "повисли". Самые
известные из них --- факторизация, дискретное логарифмирование и
изоморфизм графов.
(как в случае задачи линейного
программирования). А несколько задач, как говорится, "повисли". Самые
известные из них --- факторизация, дискретное логарифмирование и
изоморфизм графов.
Заметим, что если ![]() , то все языки
в классе
, то все языки
в классе ![]() являются полными. Так что доказать,
что какой-либо язык не является
являются полными. Так что доказать,
что какой-либо язык не является ![]() -полным, не
отделив при этом класс
-полным, не
отделив при этом класс ![]() от
от
![]() , невозможно. Но можно доказать условный
результат типа: если
, невозможно. Но можно доказать условный
результат типа: если ![]() ,
то . . . Всюду ниже, до конца обсуждения, мы
предполагаем истинной следующую гипотезу: полиномиальная иерархия не
вырождается, т. е. нетривиальна (говорят, что полиномиальная
иерархия вырождается, если для всех
,
то . . . Всюду ниже, до конца обсуждения, мы
предполагаем истинной следующую гипотезу: полиномиальная иерархия не
вырождается, т. е. нетривиальна (говорят, что полиномиальная
иерархия вырождается, если для всех ![]() , кроме конечного
числа,
, кроме конечного
числа, ![]() ,
,
![]() ).
).
Любопытно, что вопрос о вычислительной сложности задач
факторизации, дискретного логарифмирования и распознавания изоморфизма
графов интересен прежде всего с точки зрения криптографических
приложений, и именно математическая криптография дала инструмент,
позволивший, частично и условно, решить проблему их
![]() -полноты. Из теоремы Фортнау [16] и некоторых других результатов следует, что
если для какого-либо
-полноты. Из теоремы Фортнау [16] и некоторых других результатов следует, что
если для какого-либо ![]() -полного языка существует
протокол интерактивного доказательства со статистически нулевым
разглашением, то полиномиальная иерархия вырождается. Таким образом,
наличие для языка доказательства со статистически нулевым разглашением
является косвенным аргументом против его (языка)
-полного языка существует
протокол интерактивного доказательства со статистически нулевым
разглашением, то полиномиальная иерархия вырождается. Таким образом,
наличие для языка доказательства со статистически нулевым разглашением
является косвенным аргументом против его (языка)
![]() -полноты. Такие доказательства были построены
для языков ИЗОМОРФИЗМ ГРАФОВ и КВАДРАТИЧНЫЕ ВЫЧЕТЫ. Следовательно,
задача распознавания изоморфизма графов не может быть
-полноты. Такие доказательства были построены
для языков ИЗОМОРФИЗМ ГРАФОВ и КВАДРАТИЧНЫЕ ВЫЧЕТЫ. Следовательно,
задача распознавания изоморфизма графов не может быть
![]() -полной. Задача факторизации полиномиально
эквивалентна задаче извлечения квадратных корней по составному
модулю. К последней полиномиально сводима задача распознавания
квадратичных вычетов. Если бы удалось доказать полиномиальную
сводимость и в обратную сторону, то из этого следовало бы, что задача
факторизации не может быть
-полной. Задача факторизации полиномиально
эквивалентна задаче извлечения квадратных корней по составному
модулю. К последней полиномиально сводима задача распознавания
квадратичных вычетов. Если бы удалось доказать полиномиальную
сводимость и в обратную сторону, то из этого следовало бы, что задача
факторизации не может быть
![]() -полной. Альтернативно, тот же результат можно
получить, если удастся построить доказательство со статистически
нулевым разглашением для определенного выше языка
-полной. Альтернативно, тот же результат можно
получить, если удастся построить доказательство со статистически
нулевым разглашением для определенного выше языка ![]() .
.
Следует иметь в виду, что для задач из класса
![]() нет никакого "закона 0-1". Еще в
1975 г. Ладнер [17] доказал, что если
нет никакого "закона 0-1". Еще в
1975 г. Ладнер [17] доказал, что если
![]() , то в
, то в
![]() имеется бесконечно много
задач, которые не являются
имеется бесконечно много
задач, которые не являются ![]() -полными.
-полными.
В заключение отметим, что, как уже говорилось выше, вычислительная
сложность задач факторизации и дискретного логарифмирования интересна
прежде всего для криптографии. Но речь идет вовсе не о
![]() -полноте.
-полноте. ![]() -полнота ---
это сложность "в худшем случае", для криптографии слишком
слабая. Более важная и трудная задача --- обосновать, что функция
RSA и дискретная экспонента являются односторонними функциями.
-полнота ---
это сложность "в худшем случае", для криптографии слишком
слабая. Более важная и трудная задача --- обосновать, что функция
RSA и дискретная экспонента являются односторонними функциями.
3. Ну, уж этот вопрос никак нельзя назвать чисто
гипотетическим. Очень важно иметь четкое представление, что произойдет
с криптографией, если вдруг окажется, что
![]() или
или
![]() . Тем более, что, как нам
представляется, произойдет нечто из ряда вон: криптография, и
теоретическая и практическая, по существу прекратят свое
существование. "Выживут" шифры типа Вернама с одноразовыми ключами,
схемы аутентификации типа Симмонса, также с одноразовыми ключами,
схемы разделения секрета. И, по большому счету, все.
. Тем более, что, как нам
представляется, произойдет нечто из ряда вон: криптография, и
теоретическая и практическая, по существу прекратят свое
существование. "Выживут" шифры типа Вернама с одноразовыми ключами,
схемы аутентификации типа Симмонса, также с одноразовыми ключами,
схемы разделения секрета. И, по большому счету, все.
Криптографы, как правило, "с порога" отвергают этот тезис, не желая слушать никакие доводы. Тех же, кто готов данный тезис обдумывать, мы приглашаем: давайте разбираться.
Во-первых, криптография "живет" внутри класса
![]() в том смысле, что все вычислительные задачи,
возникающие перед противником, не выводят за пределы этого класса. Это
легко понять, рассматривая криптографию с открытым ключом. Противник
всегда знает открытый ключ, может угадать секретный ключ и проверить,
что он соответствует данному открытому. Ясно, что задача определения
секретного ключа принадлежит классу
в том смысле, что все вычислительные задачи,
возникающие перед противником, не выводят за пределы этого класса. Это
легко понять, рассматривая криптографию с открытым ключом. Противник
всегда знает открытый ключ, может угадать секретный ключ и проверить,
что он соответствует данному открытому. Ясно, что задача определения
секретного ключа принадлежит классу ![]() . В случае
криптографии с секретным ключом ситуация немного сложнее, надо
рассматривать различные случая и подслучаи, отсекая шифры с
шенноновской абсолютной секретностью и т. д. Но вывод тот же: все
возникающие вычислительные задачи принадлежат классу
. В случае
криптографии с секретным ключом ситуация немного сложнее, надо
рассматривать различные случая и подслучаи, отсекая шифры с
шенноновской абсолютной секретностью и т. д. Но вывод тот же: все
возникающие вычислительные задачи принадлежат классу
![]() .
.
Поскольку мы предполагаем, что ![]() или
или ![]() , для каждой задачи
из
, для каждой задачи
из ![]() имеется полиномиальный алгоритм, не суть
важно какой, детерминированный или вероятностный.
имеется полиномиальный алгоритм, не суть
важно какой, детерминированный или вероятностный.
Первое возражение против нашего тезиса обычно таково. Теория сложности работает с задачами, у которых длина входа стремится к бесконечности, и дает результаты, верные лишь асимптотически. Но во-первых, если любую вычислительную задачу рассматривать лишь на конечном начальном отрезке, то ее сложность --- константа (о константах в вычислительной сложности см. ниже). А во-вторых, можно ли представить себе естественную вычислительную задачу (не искусственно построенный пример), для которой на коротких входах все очень сложно, а с ростом длины входа задача становится все проще и проще?
Второе возражение: даже если ![]() ,
неизвестно еще, какие константы будут в полиномах. В самом деле, для
каждой задачи из
,
неизвестно еще, какие константы будут в полиномах. В самом деле, для
каждой задачи из ![]() функция сложности будет
иметь вид
функция сложности будет
иметь вид ![]() , и не важно даже, каков показатель
степени
, и не важно даже, каков показатель
степени ![]() , если эта сложность не меньше
, если эта сложность не меньше ![]() с астрономической константой
с астрономической константой ![]() .
.
Здесь очень важно понять (факт, имеющий первостепенное значение для
понимания всей криптографии), что этой константы ![]() на
самом деле нет. Предположим, мы разработали, скажем, криптосистему,
сформулировали задачу, стоящую перед противником, и доказали, что
минимальная схема из двухвходовых элементов И и ИЛИ и элементов НЕ,
решающая эту задачу, имеет сложность
на
самом деле нет. Предположим, мы разработали, скажем, криптосистему,
сформулировали задачу, стоящую перед противником, и доказали, что
минимальная схема из двухвходовых элементов И и ИЛИ и элементов НЕ,
решающая эту задачу, имеет сложность ![]() с
устраивающей нас константой
с
устраивающей нас константой ![]() . Остается лишь объяснить
противнику, что он должен пользоваться только схемами в этом базисе! В
самом деле, специалисты по синтезу схем тут же предложат другой базис,
также реализуемый на практике, в котором эта константа будет меньше. А
ведь существуют и другие модели вычислений, и поскольку при переходе
от одной модели к другой константа
. Остается лишь объяснить
противнику, что он должен пользоваться только схемами в этом базисе! В
самом деле, специалисты по синтезу схем тут же предложат другой базис,
также реализуемый на практике, в котором эта константа будет меньше. А
ведь существуют и другие модели вычислений, и поскольку при переходе
от одной модели к другой константа ![]() "плывет", любое ее
значение, даже астрономическое, создает лишь иллюзию защиты от
противника.
"плывет", любое ее
значение, даже астрономическое, создает лишь иллюзию защиты от
противника.
С показателем степени ![]() ситуация и сложнее и
интереснее. Прежде всего, приведем следующий любопытный факт: для
всякого
ситуация и сложнее и
интереснее. Прежде всего, приведем следующий любопытный факт: для
всякого ![]() существует функция, вычислимая (на
детерминированной машине Тьюринга) за время
существует функция, вычислимая (на
детерминированной машине Тьюринга) за время ![]() и
не вычислимая за время
и
не вычислимая за время ![]() (теорема об иерархии).
Истинность этого утверждения не зависит ни от каких недоказанных
предположений, в частности от решения проблемы о соотношении классов
(теорема об иерархии).
Истинность этого утверждения не зависит ни от каких недоказанных
предположений, в частности от решения проблемы о соотношении классов
![]() и
и ![]() . Почему бы не
попытаться использовать эти доказуемо очень сложные функции в
криптографии? Дело в том, что теорема об иерархии доказывается
диагональным методом и для всех доставляемых ею функций нет более
простого описания, чем определяющий их диагональный
процесс. Математики же обычно имеют дело с естественными задачами,
имеющими короткие и простые описания, такими как известные
. Почему бы не
попытаться использовать эти доказуемо очень сложные функции в
криптографии? Дело в том, что теорема об иерархии доказывается
диагональным методом и для всех доставляемых ею функций нет более
простого описания, чем определяющий их диагональный
процесс. Математики же обычно имеют дело с естественными задачами,
имеющими короткие и простые описания, такими как известные
![]() -полные задачи, задача факторизации, задача
дискретного логарифмирования и т. п. Так вот, на данный момент не
известно ни одной естественной задачи, для решения которой был бы
найден полиномиальный алгоритм высокой степени и эта степень не
поддавалась бы снижению. Типичные значения показателя степени
-полные задачи, задача факторизации, задача
дискретного логарифмирования и т. п. Так вот, на данный момент не
известно ни одной естественной задачи, для решения которой был бы
найден полиномиальный алгоритм высокой степени и эта степень не
поддавалась бы снижению. Типичные значения показателя степени
![]() для естественных задач ---
для естественных задач ---
![]() ,
, ![]() ,
, ![]() . Можно
предположить, что для естественных задач действует своего рода
закон 0-1: сложность задачи либо сверхполиномиальна, либо
ограничена сверху полиномом невысокой степени. За последнее время это
предположение неоднократно высказывалось в качестве научной гипотезы,
пока на неформальном уровне.
. Можно
предположить, что для естественных задач действует своего рода
закон 0-1: сложность задачи либо сверхполиномиальна, либо
ограничена сверху полиномом невысокой степени. За последнее время это
предположение неоднократно высказывалось в качестве научной гипотезы,
пока на неформальном уровне.
Литература
- Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982.
- Китаев А. Ю., Шень А. Х., Вялый М. Н. Классические и квантовые вычисления. М.: МЦНМО, 1999.
- Lautemann C.
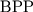 and the polynomial hierarchy. Inf. Process. Letters, 17, N 4,
1983, 215--217.
and the polynomial hierarchy. Inf. Process. Letters, 17, N 4,
1983, 215--217.
- Shaltiel R., Umans C. Simple extractors for all min-entropies and a new pseudo-random generator. FOCS'42, 2001.
- Baker T. P., Gill J.,
Solovay R. Relativizations of the
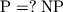 question. SIAM
J. Comput., 4, N 4, 1975, 431--442.
question. SIAM
J. Comput., 4, N 4, 1975, 431--442.
- Heller H. On relativized exponential and probabilistic complexity classes. Information and Computation, 71, 1986, 231--243.
- Zwick U. A
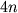 lower bound
on the combinational complexity of certain symmetric Boolean functions
over the basis of unate dyadic Boolean functions. SIAM J. Comput., 20,
1991.
lower bound
on the combinational complexity of certain symmetric Boolean functions
over the basis of unate dyadic Boolean functions. SIAM J. Comput., 20,
1991.
- Разборов А. А. Нижние оценки монотонной сложности некоторых булевых функций. Доклады АН СССР, 281, N 4, 1985, 798--801.
- Андреев А. Е. Об одном методе получения эффективных нижних оценок монотонной сложности. Доклады АН СССР, 282, N 5, 1985, 1033--1037.
- Furst M., Saxe J., Sipser M. Parity, circuits and the polynomial time hierarchy. Math. Systems Theory, 17, 1984, 13--27.
- Ajtai M.
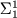 -formulae on finite structures. Annals of Pure
and Applied Logic, 24, 1983, 1--48.
-formulae on finite structures. Annals of Pure
and Applied Logic, 24, 1983, 1--48.
- Yao A. C. Separating the polynomial-time hierarchy by oracles. FOCS'26, 1985, 1--10.
- Håstad J. Computational limitations for small depth circuits. MIT Press, 1986.
- Schroeppel R., Shamir A. A
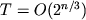 ,
, 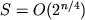 algorithm for
certain
algorithm for
certain 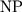 -complete problems. SIAM J. Comput.,
10, N 3, 1981, 456--464.
-complete problems. SIAM J. Comput.,
10, N 3, 1981, 456--464.
- Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. М.: МЦНМО, 2003.
- Fortnow L. The complexity of perfect zero-knowledge. STOC'19, 1987, 204--209.
- Ladner R. On the structure of polynomial time reducibility. J. of the ACM, 22, N 1, 1975, 155--171.